√ 張り出し梁 モーメント 114154

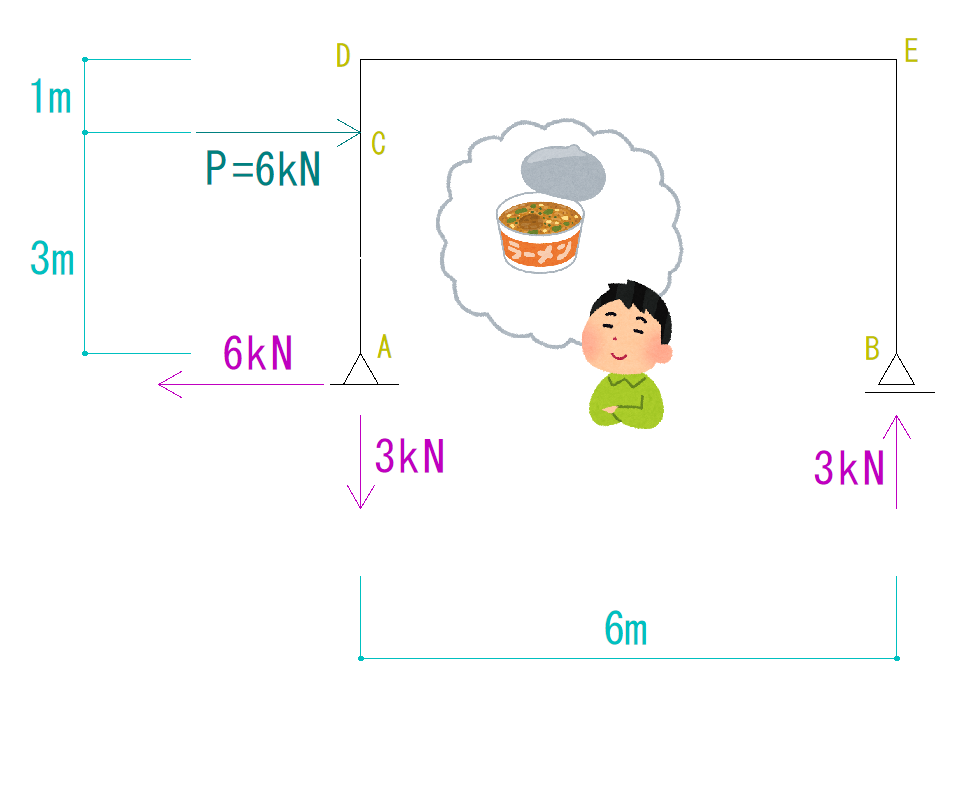
4 モールの定理によれば、上記の荷重に対して、梁中央の曲げ モーメントがこの単純梁の載荷点における鉛直変位である。 図105において、w は三角形部分の分布荷重の合力、 c m が 梁中央での曲げモーメントである。分布荷重の合力w は におき直し、反力 梁などを途中で切った場合に、曲げモーメントm x とせん断力q x が作用する ということです。 切った左側はこのようになります。 そして切った右側もこのようになります。1 72 7 (2) 72kN 30kN 3m 30 1 90kN 1/2 14 VB o 3m 42kN 30 4m 3m 30kN 3m 4m NJ / 03 k" y 140 3' 2 1 37 3b' 72 36 1 —

第８章 構造解析法への適用

張り出し梁 モーメント

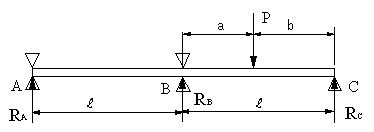
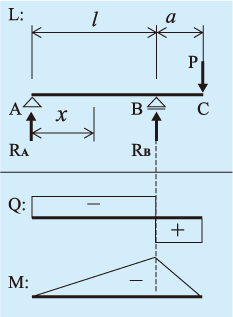
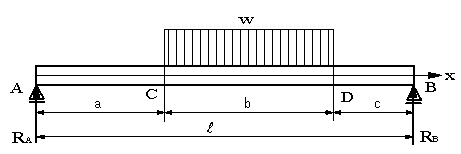
張り出し梁 モーメント- 支点に生じる反力を力のつりあいの3条件で解けるものを静定梁、 力のつりあい条件だけでは解けないものを不静定梁といいます。 作用する荷重に対して、支点に生じる反力を求めること、 求めた反力により梁部材に生じる断面力 ・曲げモーメント 張り出し梁の最大曲げモーメント 例えば 全長9m 中央支持間5m 両端2mづつの張り出しがある梁に 等分布荷重10kg/m の荷重が掛かっている時の曲げモーメントは 中央部で 1125kg m 張り出しの支持点で kg mとなりますが この場合、最大応力は中央部で見るのでしょうか？

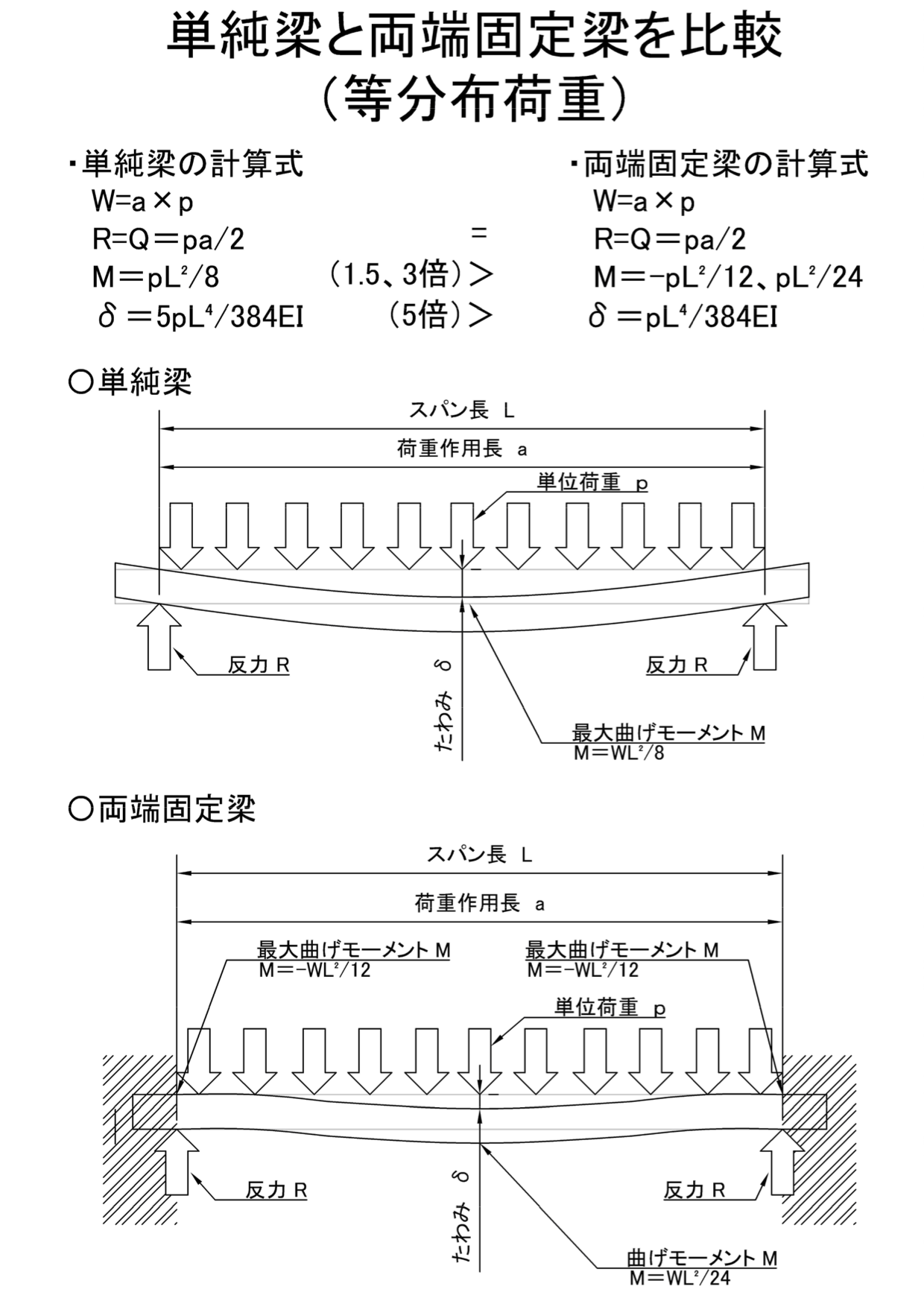
単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督

合、静的モーメントが各方向で許容値内であることを確 認する必要があります。 442 動的許容モーメント 電動スライダがワークを搬送している場合に作用する モーメントを動的モーメントといいます。運転時に加速 張り出し梁の反力の作用点について。 以下のような図（といっても粗末だが）に力Fが加わっています。 や は支持の箇所で、―――は梁です。 （もちろん支持は梁に密着） このとき、反力が作用する点は支持Aはもちろんですが、右端は支持Cだけなのか 共役梁に弾性荷重を載せると、せん断力を求めるようにたわみ角が求まり、曲げモーメントを求めるようにたわみが求まるのです。 こちらも求積法が使えるので、比較的簡単に求めることができます。 共役梁 共役梁にはルールがあります。 単純梁はその

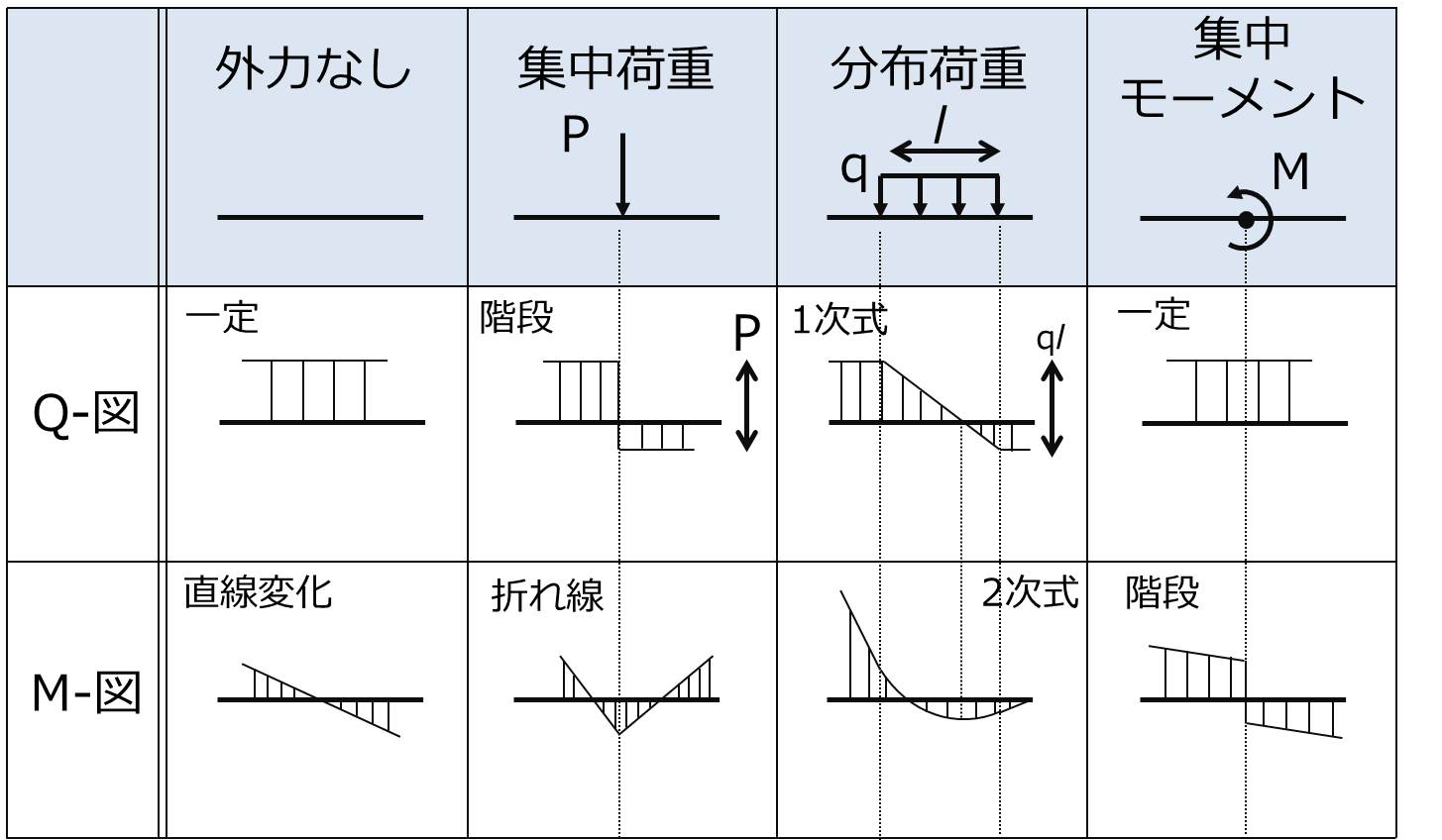
両端固定梁 モーメントを任意の位置に付加 せん断 力 荷重 モーメント 荷重 せん断 力 モーメント xaの時 しかし x5 片持ち梁のたわみとたわみ角 51 ③片持ち梁の集中荷重; 曲げモーメント図は、集中荷重が作用する場合、点a~c間、点c~d間、点d~b間で 一定の傾きを持った直線 となります。 また、単純ばりのピン支点、ローラー支点では回転は拘束されないので、 端部の点a、点bでは曲げモーメントは0になる こともポイントです。

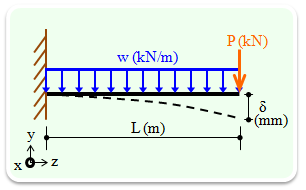
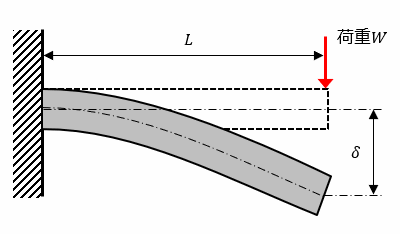
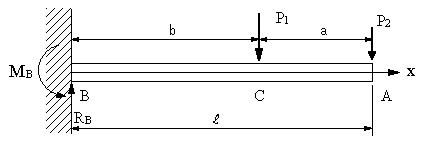
梁端部 H700x 300x14 x28 ノンスカ ラップ 溶 接 ダイヤフ ラム SN490C 厚36 柱：BCP 325 700x 700x25 FPL S N490B t=25,30 0x600 H TB 2x3 M 24 WPL t= 16,300x 600 HTB 2x 6 M24 外壁受 け 100 x50 計算書 Ⅰ) 設計全体の流れ 基本設計案が建築主に承認されると 実施設計に入ります。実片持ち梁とは 片持ち梁とは壁から梁が飛び出した構造である。 ジブクレーンが代表的な例である。片方の端部を「固定」し、他端は自由端である。 梁の種類 梁は支点条件により3種類に分類することができる。 「単純梁」と「両端固定梁」と「片持ち梁」である。梁の公式 荷重・形状 条件 曲げモーメント m反力 r･せん断力 q･全荷重 w たわみ δ P l Rb a b w＝p rb＝p qb＝－p mb＝－pl pl3 δa＝ 3ei l Rb a b P1 P2 abrb＝p1＋p2 qb＝－（p1＋p2） w＝p1＋p2 mb＝－（p1l＋p2b） 2 δa＝ ＋ 3ei p1l3 6ei p2b （3l－b） l Rb a b ab P w＝p rb＝p

第８章 構造解析法への適用

力のモーメントの問題で 図に示す曲がりはりの先端に 大きさ8 Yahoo 知恵袋

単純梁 両端ピン ← 図をクリックすると、 各種計算式が表示されます。 反力、せん断、曲げモーメント、 たわみ、・・・ Type ピン－固定 中心集中荷重 ピン－固定 偏芯集中荷重 ピン－固定 等分布荷重 ピン 固定梁 ← 図をクリックすると、42 ②単純梁の等分布荷重 421 覚えておくポイントその2;②梁自重（地震時慣性力）による作用力 ③風荷重による作用力 ④任意荷重による作用力 照査位置 曲げモーメント照査位置 鉛直方向の計算に準じます。 せん断照査位置 梁付け根位置と各支承位置で照査を行います。 照査断面 L1 L 2 d o '

4 5 影響線

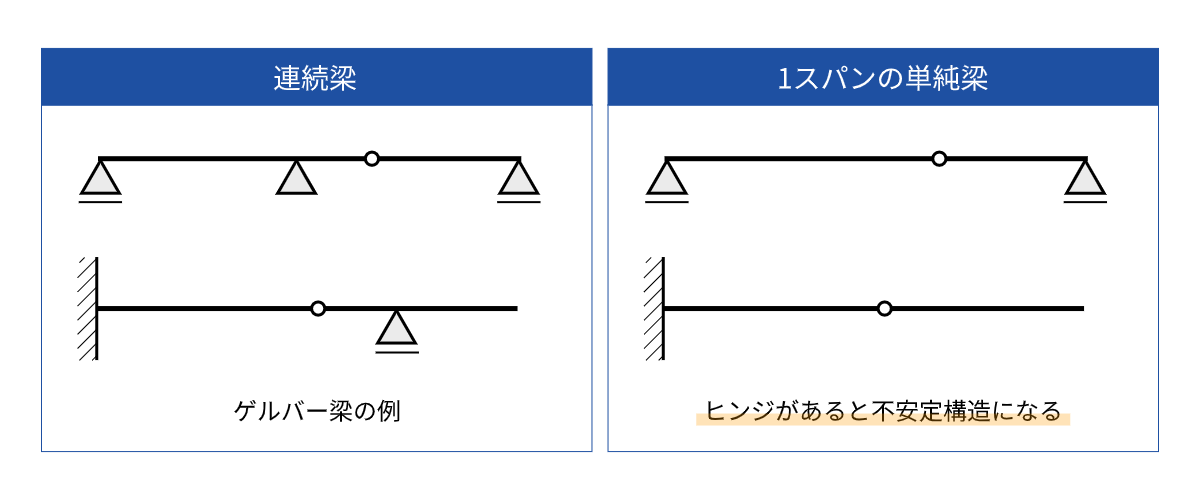
構造力学の基礎 ゲルバー梁 第回 ゆるっと建築ライフ

梁のせん断力と曲げモーメントに関する理解度を確認する為に簡単なテストを実施する． 2 丸棒のねじり 丸棒のねじりによるせん断応力の計算法について補足する． 3 梁の曲げ応力 曲げ応力の概念と計算法，曲げ応力と合応力としての曲げモーメントとのWebFUNX 断面性能 材料・許容応力度 荷重・外力 応力計算 0121 temmakozo co,ltdモーメント荷重が作用する単純梁の 反力 曲げモーメント たわみ の求め方について説明します。モーメント荷重の詳細は、下記が参考になります。 モーメント荷重とは？1分でわかる意味、片持ち梁のモーメント図と計算方法

はりの曲げモーメントせん断力解説

Ogtp4xerm Com Oas Php

梁の曲げモーメント ( M ) , 反力 片持ち 両端支持 両端固定 張り出し ・荷重 ( 集中荷重／均等分布荷重／部分分布荷重／モーメント )‐梁の長さより曲げモーメントとH Hamano， 6 はりの影響線 61 61 はりの影響線 「任意点の断面力を単位集中荷重P=1 の作用位置で表し，単位集中荷重P=1 を移動させてその縦距 を連ねた線」を影響線という．ここに，断面力は反力，せん断力，曲げモーメントを意味する．の一次式，曲げモーメントは x の二次式となり，例題 51 の集中荷重の場合よりも一 次だけ次数が上がる． 支点上で曲げモーメントは0 となる（境界条件参照）． せん断力が0 となる点 (Q x 0) で曲げモーメントは極値をとることに注意． 式(a)で Q x M 0 とおく

Http Shake Tu Chiba U Jp Lecture Strmcni Pdf Stri Note 12 Pdf

連続梁の反力の算出がうまく出来ません 現在 図のような等分布荷重を 物理学 教えて Goo

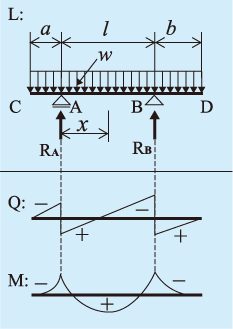
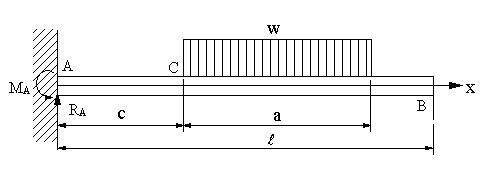
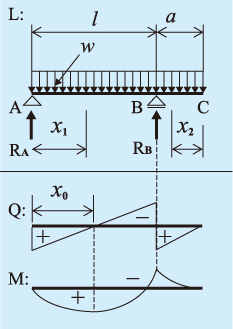
梁の微分方程式 複雑な梁の応力解析 図131に、片持ち梁の中央に支持点がある不静定構造物を示す。この 構造物の曲げモーメントとせん断力を求め、さらに、変形を求めること にする。 まず、b～c間の梁について考える。この部分は片持ち梁となっている図に示すような両側にl 1 、l 2 の張り出しをもつ両端突出はりがある。ただし、P 1 ＞P2、l 1 ＞l 2 とし、xはC点を原点に取る。 ①CA間、AB間、BD間のせん断力Vx、曲げモーメントMxを求める。 ②最大曲げモーメントM max と、M max が生ずる位置(Cより右向きにとる 転倒モーメントがわかる：重心位置との関係と計算方法について 構造設計：実務 建物が地震で倒れるのは、柱や梁が損傷して重さを支えられなくなるからです。 ですので、柱や梁を地震に耐えられるよう頑丈にすれば問題は解決します。 しかし、どれ

第８章 構造解析法への適用

単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督

 また、最大せん断応力度τmaxは部材断面形状により異なるが、円形断面の場合にはτmax＝( ）、で計算する事ができる。 長さ （決まってません）の単純梁の中央に集中荷重Pが作用した場合、曲げモーメントMが最大となる位置は もちろん強度はそこそこありますが、張り出しの部分が大きくなればなるほど、モーメント力(支点を回す力)が大きくなっていきます。 今後、片持梁はよく出てくるのでしっかりと理解しておきましょう。 片持梁の反力の解説 では例題から考えていき 曲げモーメント自体が作用している梁の問題 も結構出題されています。 作用している曲げモーメントの考え方を知らないと手が出なくなってしまうので、実際に出題された基礎的な問題を一問解いていきます。 ⑤曲げモーメントが作用している梁のせん断

10 号 梁構造 Astamuse

Ex 5

図の梁の場合に、たわみの式と、最大たわみを求める。 ac,db部分の梁の断面二次モーメントi 1,とし、cd部分の梁の断面二次モーメントi 2 とし、弾性係数はいずれもeである。 解答例 問題178M：曲げモーメント図 W：全荷重 M：曲げモーメント R：反力 θ：回転角 Q：せん断力 δ：たわみ はね出し 単純梁 両端集中 荷重 はね出し 単純梁 全体分布 荷重 kanpro 公式集－梁構造ListX = 0は単純支持点なので曲げモーメントは零ですね。次にCB間で考えれば、新たに荷重P による曲 げモーメントが加わります。荷重P による曲げモーメントはP(x−l1) です。この曲げモーメントは新しい定 義によれば負です。したがって、 MCB = R1x−P(= 2 = (=() (7)

連続はり

はりの曲げモーメントせん断力解説

梁のたわみと応力計算ツール 関連ページ 機械設計で使う単位一覧 数学の公式一覧 力学の公式一覧 単位換算ツール カンタン重量計算（金属、非鉄金属、樹脂、木材など） シリンダ推力計算ツール 複合形状の断面2次モーメント計算ツール固定支点（モーメント反力） 22 荷重によるモーメントに対して モーメント反力が生じる可能性 モーメント反力 の正体は 上下から 抵抗する偶力内容： モーメントエリア法とマコーレー法 マコーレーの方法 定義 マコーレーのたわみ角法 マコーレーの方法の例1： 単純に支持された梁の傾斜とたわみ for均一に分散された負荷 マコーレーの方法の例2：張り出した梁の勾配とたわみ モーメントエリア

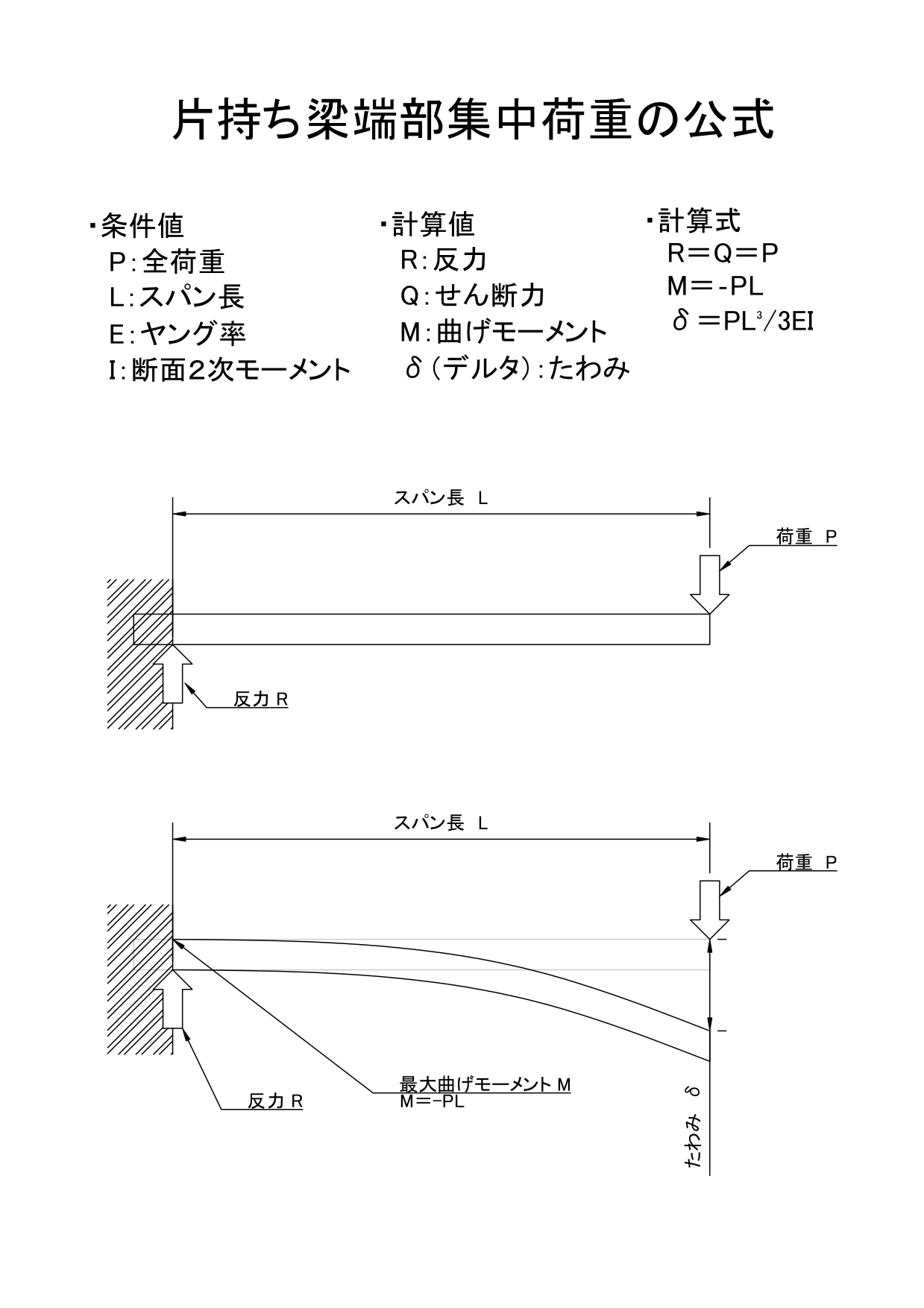
公式集 構造計算 片持ち梁 曲げモーメント せん断 反力 たわみ

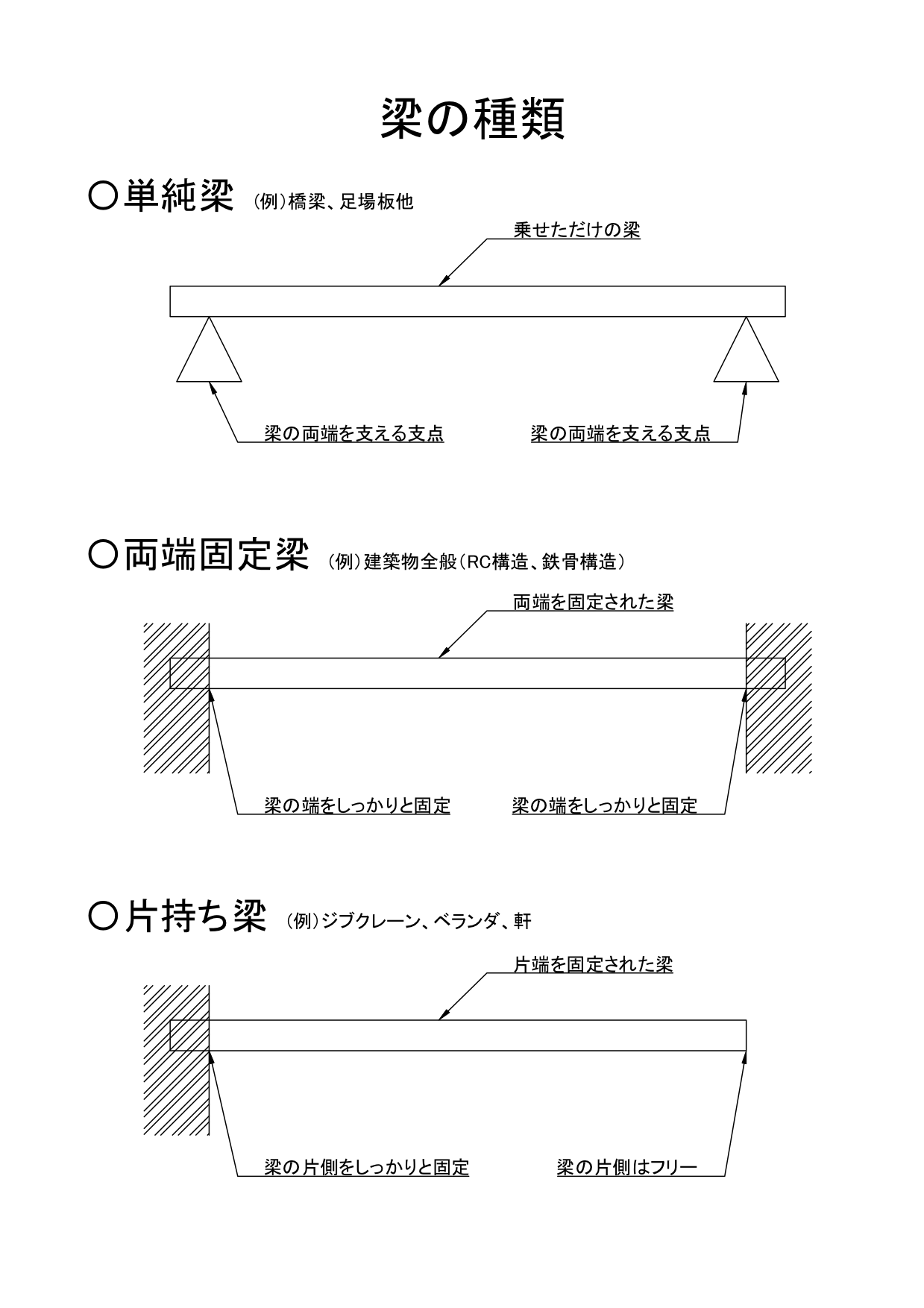
片持ち梁とは 張出し構造 機械卒でも土木の現場監督

また張り出し梁 右図255のように， スパン中央に集中外力モーメント を受ける単純梁を，微分方程式を 用いて解け。 最新版を正確に読むためには pdf ファイル をどうぞ。これは web 検索のための53 ⑤片持ち梁のモーメント 531 覚えて

片持ち梁とは 張出し構造 機械卒でも土木の現場監督

2 3 静定梁

1

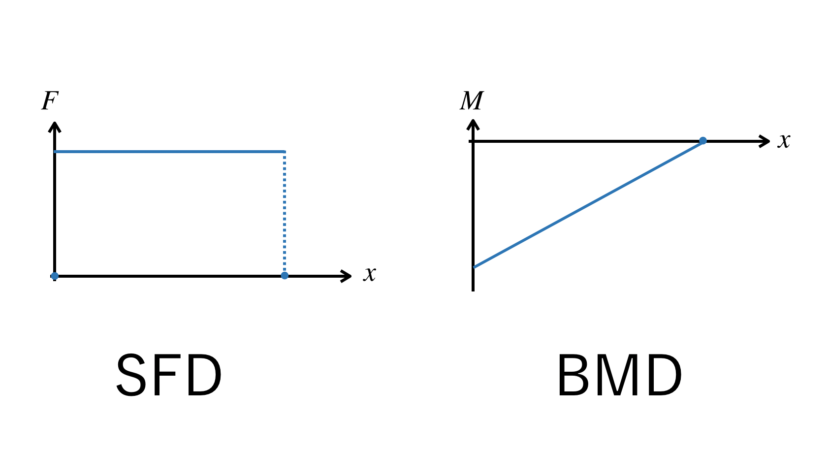
梁にかかる荷重と Sfd Bmdの作り方 ものづくりのススメ

梁の曲げモーメント図の描き方を 解きながら順番に説明します Youtube

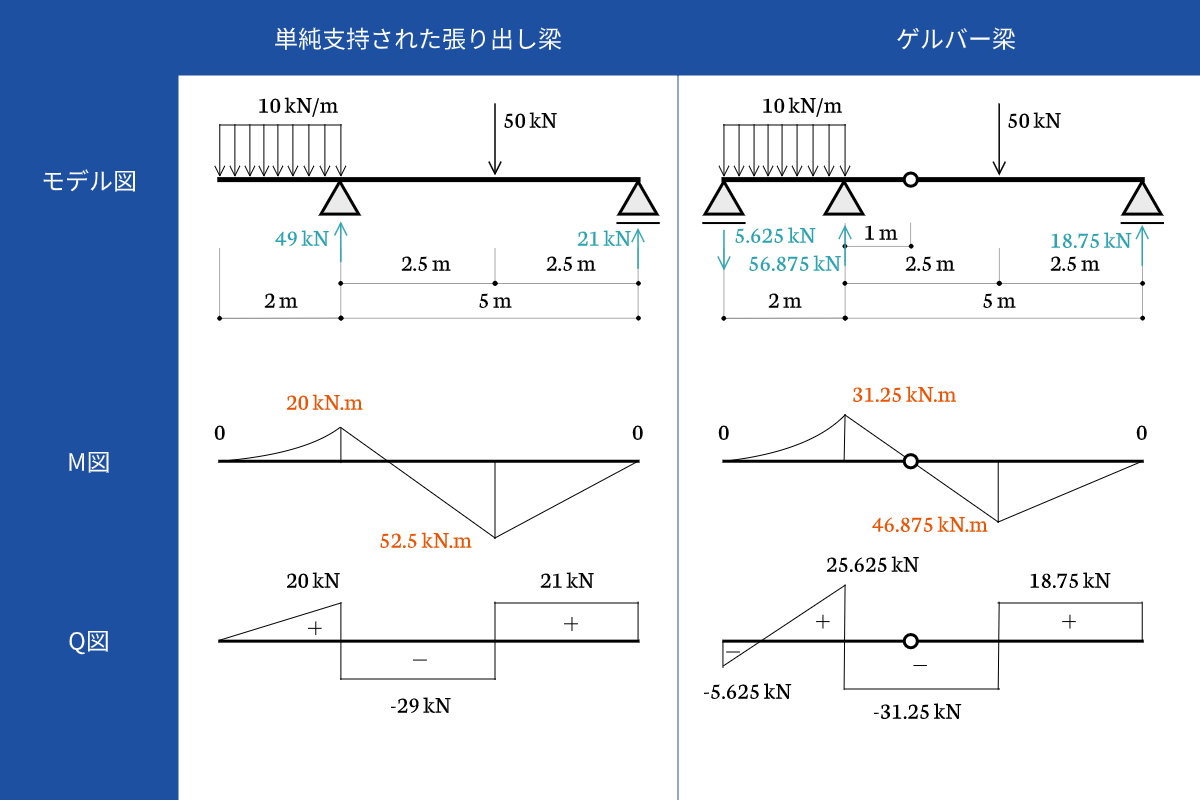
構造力学の基礎 ゲルバー梁 第回 ゆるっと建築ライフ

はねだし単純梁の曲げモーメントの出し方を教えてください 添付し Yahoo 知恵袋

梁の公式計算 水管橋設計支援ソフト 管太郎

構造計算 両側はね出し単純梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社

はりの種類と荷重の分類

構造計算 片側はね出し単純梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社

梁について 突出梁において 中央のスパンに負の曲げモーメントが存在しな Okwave

Ex 5

曲げモーメント図の書き方 両端支持梁の場合はどうなる 建築学科のための材料力学

片持ち梁の強度 変形計算 H形鋼 株式会社datエンジニアリングサービス 仮設建築物 構造物の設計 強度計算 構造計算 Fem解析等を専門に請負

断面２次モーメントによる はり のたわみ量計算

はりのひずみの計算式 共和電業

6

Ex 5

Ex 5

静定梁 せいていばり ってなに いまさら訊けない建築構造力学

構造計算 片側はね出し単純梁 切削 樹脂 プレス レーザー加工の特急試作なら日新産業株式会社

やさしい実践 機械設計講座

断面力図の描き方 基本から早く簡単な描き方 コツなど

片持ち梁の曲げモーメント図は 1分でわかる書き方 公式 計算 三角分布荷重との関係

わかりやすい 詳細 等分布荷重を受ける片持はりのたわみ

ゲルバー梁とは 1分でわかる意味 解き方 利点と単純梁との違い 応力 静定構造物との関係

はりの曲げモーメントせん断力解説

はりの曲げモーメントせん断力解説

モーメント荷重とは 1分でわかる意味 片持ち梁のモーメント図と計算方法

わかりやすい 詳細 等分布荷重を受ける片持はりのたわみ

曲げモーメント図の書き方 両端支持梁の場合はどうなる 建築学科のための材料力学

やさしい実践 機械設計講座

両端支持はりの計算 はりのたわみ計算 オンライン

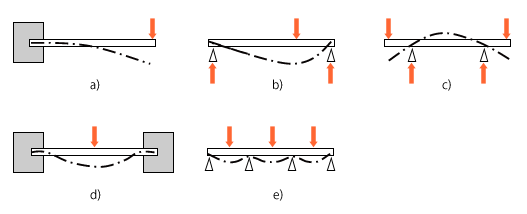
片持梁 ラーメン構造の反力の求め方 そもそもラーメン構造とは 例題から計算方法を理解しよう ネット建築塾

両端固定梁とは 1分でわかる意味 曲げモーメント たわみ 解き方

この張り出した梁が モーメントで 柱のないお堂を形成する Picture Of Aizendo Taketa Tripadvisor

Ex 5

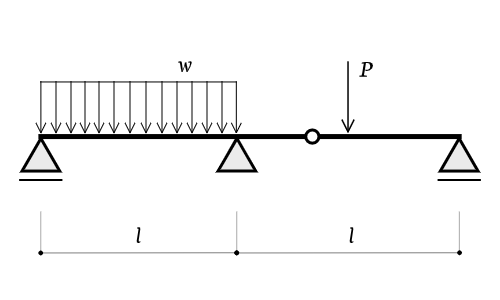
構造力学の基礎 ゲルバー梁 第回 ゆるっと建築ライフ

第８章 構造解析法への適用

はり構造と曲げ 機械工学と自動機設計 15 技術情報 Misumi Vona ミスミ

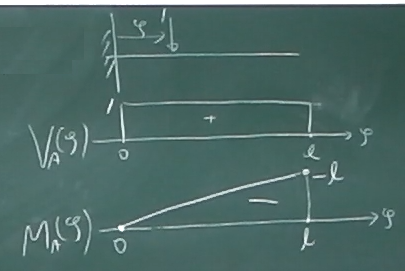
構造力学i第12回

両側はね出し単純梁の計算公式 等分布荷重

1

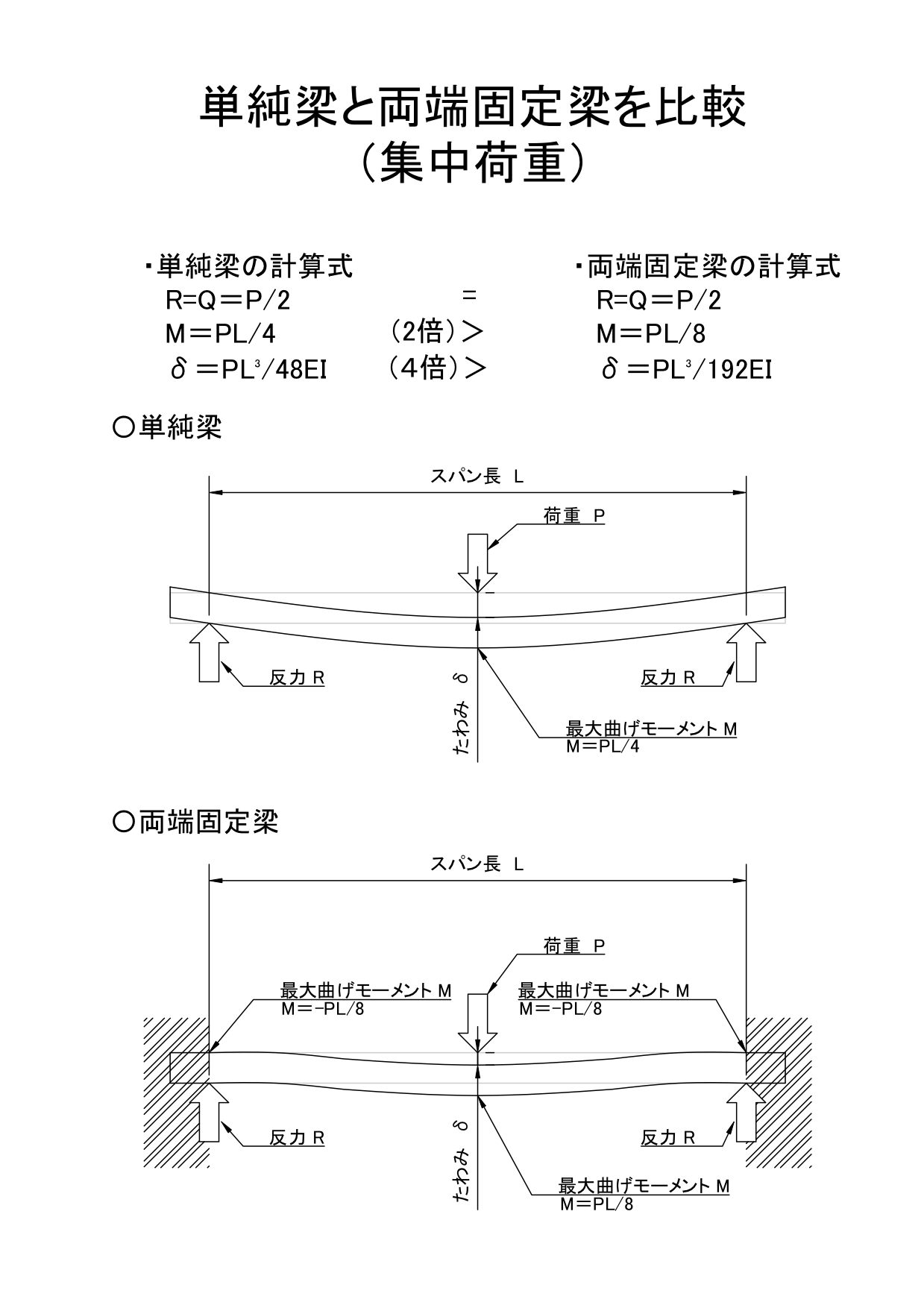
単純梁と両端固定梁を比較 単純梁の方が変位が大きい 機械卒でも土木の現場監督

曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会

15 3264号 梁および柱 梁構造 Astamuse

やさしい実践 機械設計講座

超初心者向け 材料力学のsfd せん断力図 書き方マニュアル のぼゆエンジニアリング

公式集 構造計算 片持ち梁 曲げモーメント せん断 反力 たわみ

Ogtp4xerm Com Oas Php

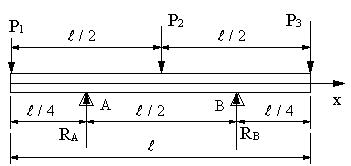
Ex 5

両端支持梁に集中荷重 2か所 の場合の最大応力 両端支持の梁に2か所 物理学 教えて Goo

曲げモーメント図の書き方 両端支持梁の場合はどうなる 建築学科のための材料力学

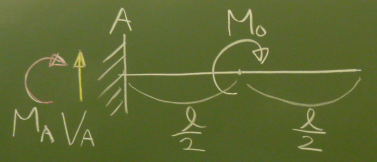
構造力学i第9回

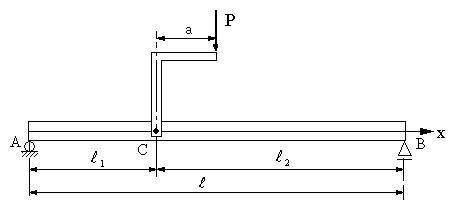
Ex 5

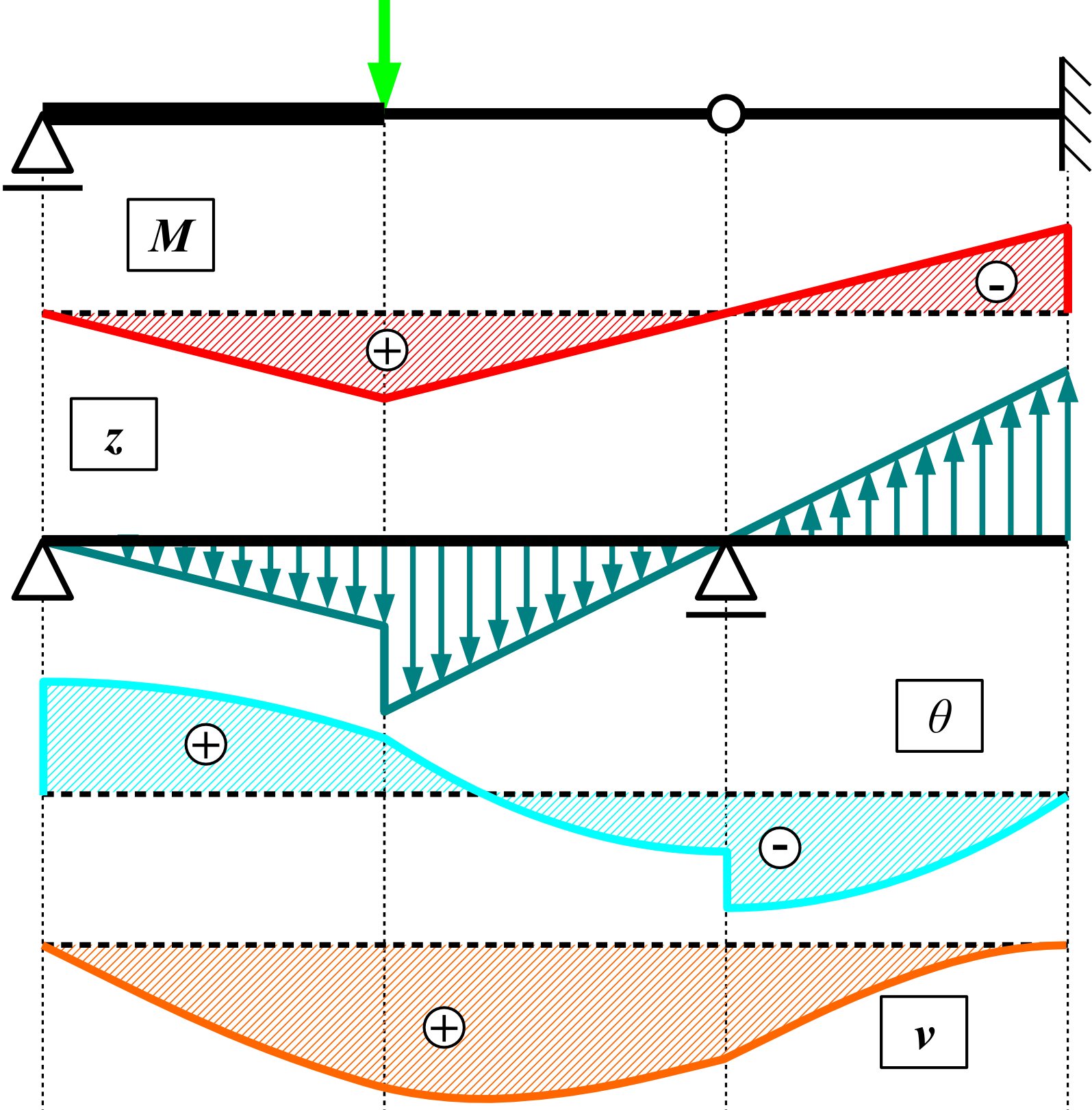
モールの定理 Wikipedia

2 3 静定梁

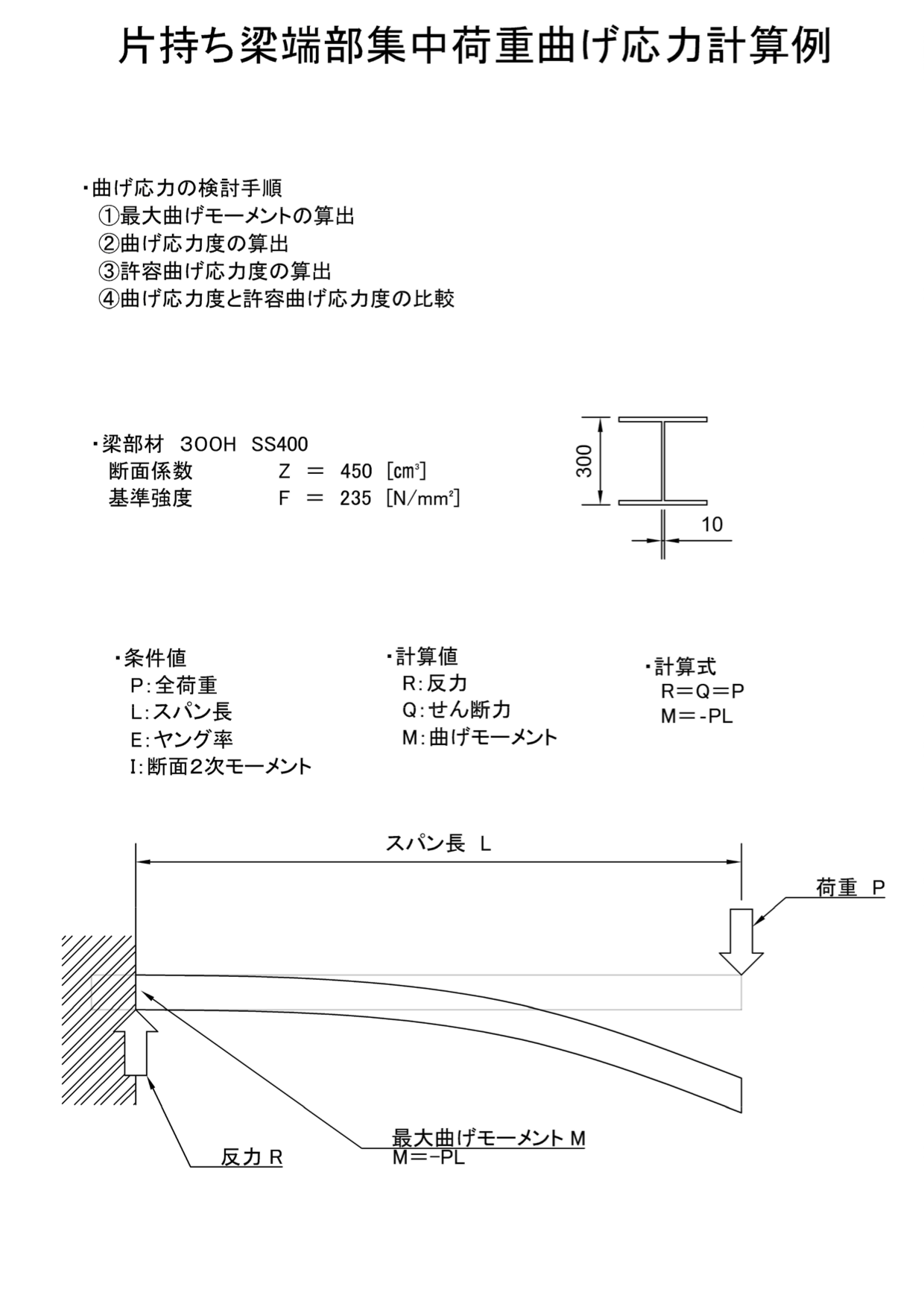
片持ち梁曲げ応力計算例 H300 集中荷重 機械卒でも土木の現場監督

はりの曲げモーメントせん断力解説

Www Jp Omega Com Techref Pressure43 67 Pdf

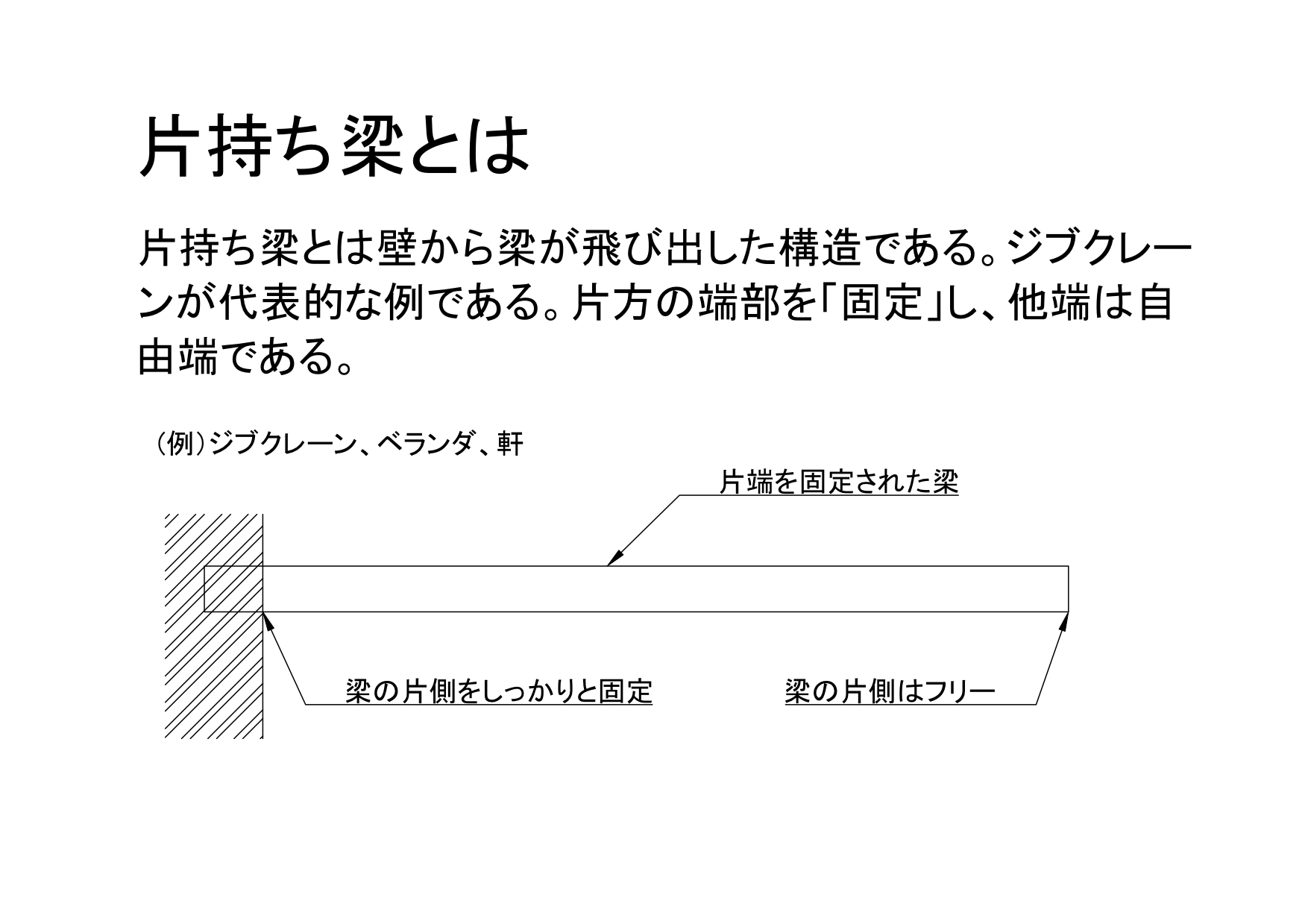
片持ち梁とは 張出し構造 機械卒でも土木の現場監督

構造力学入門 反力編04 単純梁4 Youtube

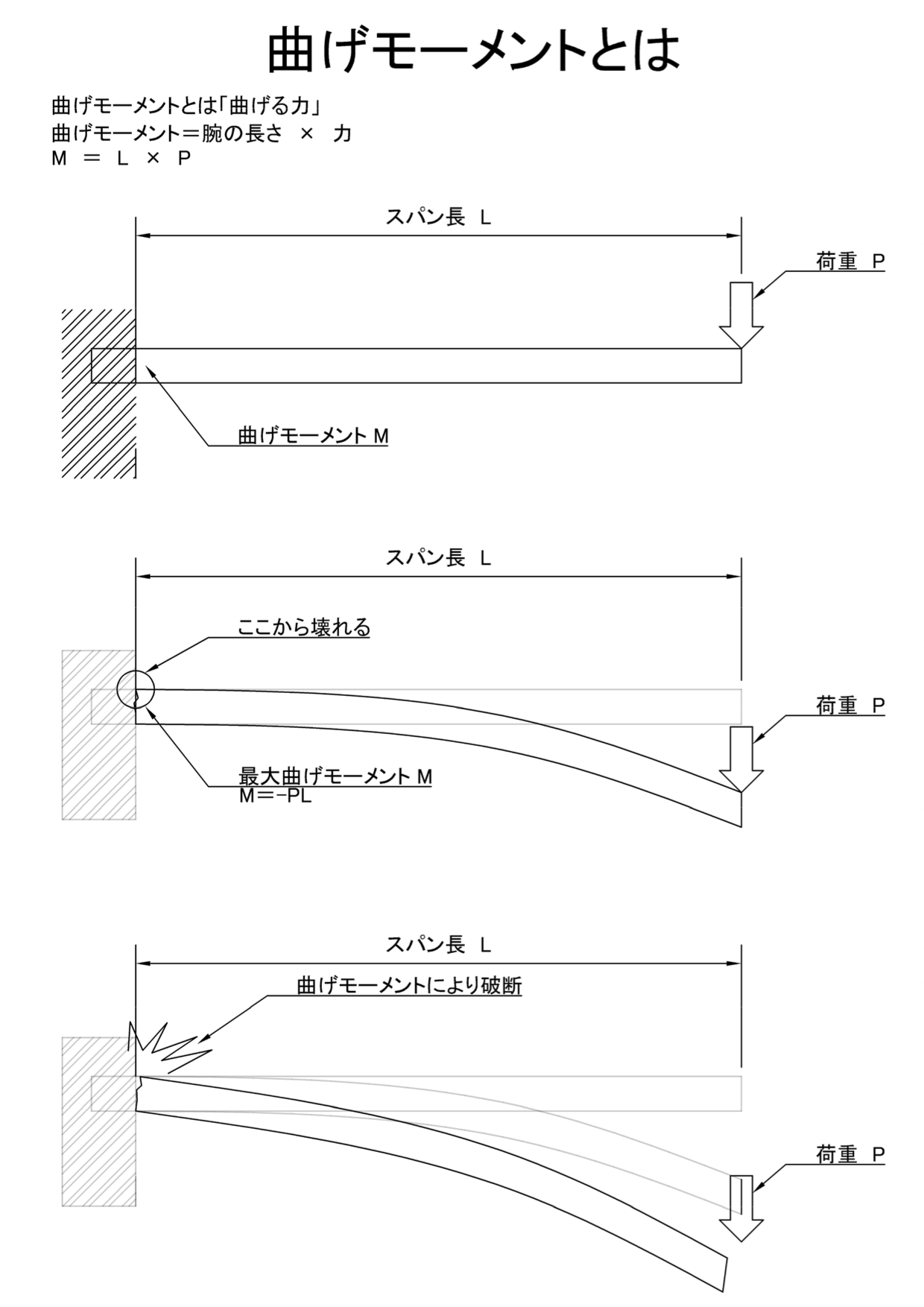
曲げモーメントとは 曲げる力 機械卒でも土木の現場監督

はね出し単純梁についての質問です 図のような構造の場合モ Yahoo 知恵袋

18 号 柱梁接合構造及びラーメン構造体 Astamuse

静定梁 せいていばり ってなに いまさら訊けない建築構造力学

過去問h28国家一般職 高卒 技術 No62解説 公務員試験 これでok

最大曲げモーメントとは 1分でわかる意味 求め方と例題 集中荷重 片持ち梁 両端固定梁の計算

Www Jp Omega Com Techref Pressure43 67 Pdf

ガチ土木

2点集中荷重片持ち梁について 2点集中荷重片持ち梁の曲げモーメントと 数学 教えて Goo

1

はり 梁 上部からの荷重をささえる 材料力学 Hitopedia

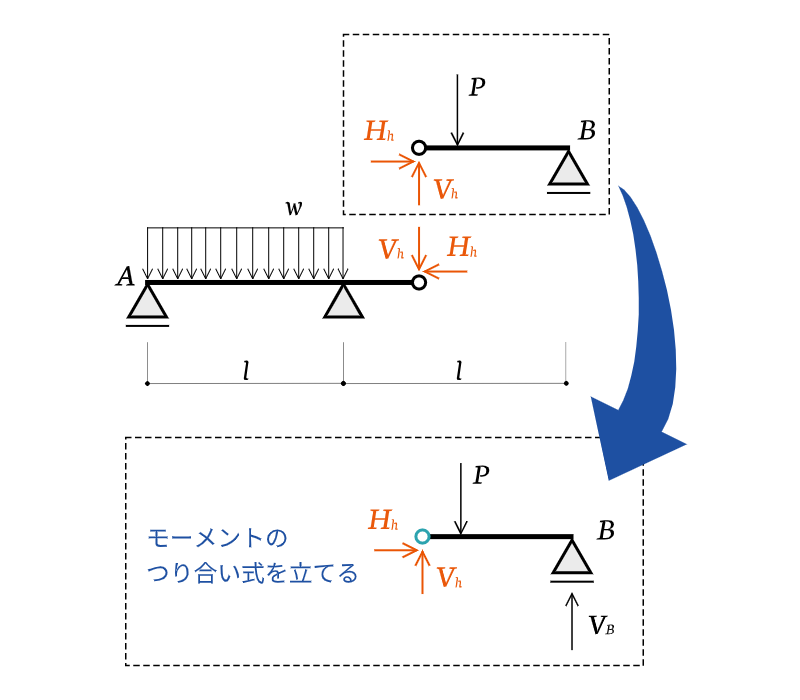
構造力学の基礎 ゲルバー梁 第回 ゆるっと建築ライフ

片持ち梁の先端にm荷重がかかった場合ですがなぜ回転を与えただけで Yahoo 知恵袋

3

公式集 構造計算 片持ち梁 曲げモーメント せん断 反力 たわみ

梁の曲げモーメント図の描き方を 解きながら順番に説明します Youtube

第８章 構造解析法への適用

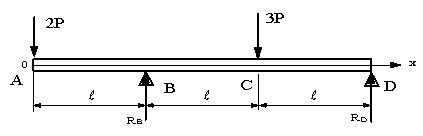
材料力学の張り出し梁の問題を教えていただきたいです 反力ra Yahoo 知恵袋

等分布荷重の計算と公式は 1分でわかる公式 計算方法 反力の求め方

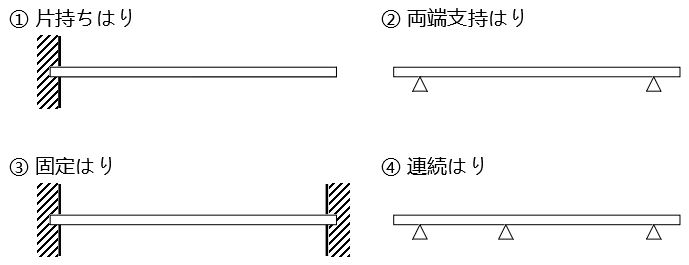
はりの種類と荷重の分類

モールの定理 Wikipedia

ゲルバー梁とは 1分でわかる意味 解き方 利点と単純梁との違い 応力 静定構造物との関係

曲げモーメント せん断力 たわみの計算式 県木連のホームページ 一般社団法人愛知県木材組合連合会

はりのせん断力 曲げモーメント たわみ量算出の公式 木のいえづくりセミナーweb版

4 3 重ね合わせの原理で不静定梁を解く